if the charge on an isolated spherical conductor is doubled, what happens to its capacitance?

Capacitance

49 Capacitors and Capacitance

Learning Objectives

By the terminate of this section, you will be able to:

Explain the concepts of a capacitor and its capacitance
Describe how to evaluate the capacitance of a system of conductors

A capacitor is a device used to store electrical charge and electric free energy. It consists of at to the lowest degree two electrical conductors separated by a distance. (Note that such electric conductors are sometimes referred to as "electrodes," but more correctly, they are "capacitor plates.") The space between capacitors may simply be a vacuum, and, in that case, a capacitor is then known as a "vacuum capacitor." However, the space is usually filled with an insulating material known as a dielectric. (Y'all will acquire more about dielectrics in the sections on dielectrics later in this chapter.) The amount of storage in a capacitor is determined by a belongings chosen capacitance, which you lot will acquire more nigh a flake later in this section.

Capacitors have applications ranging from filtering static from radio reception to energy storage in centre defibrillators. Typically, commercial capacitors take two conducting parts close to one another merely not touching, such equally those in (Figure). Most of the time, a dielectric is used between the two plates. When battery terminals are connected to an initially uncharged capacitor, the battery potential moves a pocket-size amount of charge of magnitude Q from the positive plate to the negative plate. The capacitor remains neutral overall, but with charges $+Q$ and $\text{−}Q$ residing on opposite plates.

Both capacitors shown hither were initially uncharged before being continued to a battery. They now take charges of $+Q$ and $\text{−}Q$ (respectively) on their plates. (a) A parallel-plate capacitor consists of two plates of opposite charge with area A separated past distance d. (b) A rolled capacitor has a dielectric textile betwixt its two conducting sheets (plates).

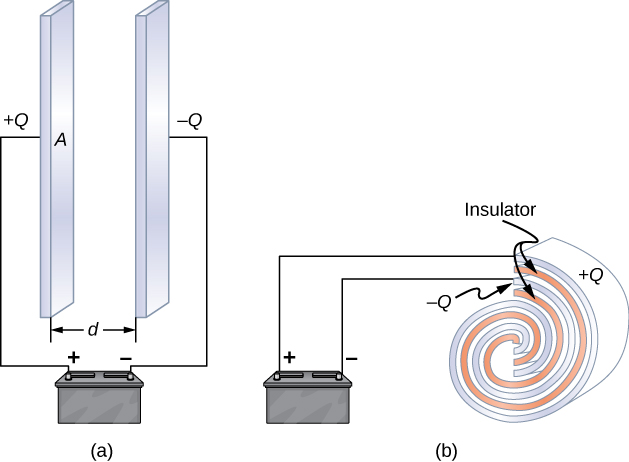
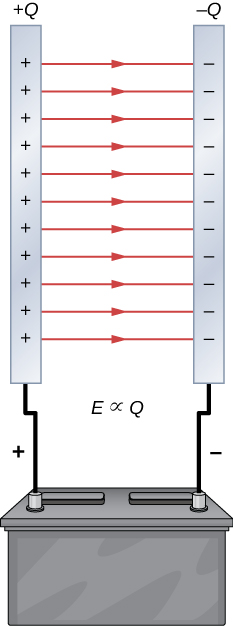
A system composed of two identical parallel-conducting plates separated by a distance is called a parallel-plate capacitor ((Figure)). The magnitude of the electrical field in the space between the parallel plates is $E=\sigma \text{/}{\epsilon }_{0}$ , where $\sigma$ denotes the surface charge density on one plate (recall that $\sigma$ is the charge Q per the expanse A). Thus, the magnitude of the field is directly proportional to Q.

The charge separation in a capacitor shows that the charges remain on the surfaces of the capacitor plates. Electric field lines in a parallel-plate capacitor begin with positive charges and finish with negative charges. The magnitude of the electric field in the space between the plates is in direct proportion to the corporeality of charge on the capacitor.

Two parallel plates are connected to a battery. The plate connected to the positive terminal has positive charges on it marked by the plus sign. Similarly, the other plate has minus signs on it. Arrows are shown between the plates, from the positive plate to the negative one. The space between the plates has the formula E proportional to Q.

Capacitors with different concrete characteristics (such equally shape and size of their plates) store different amounts of accuse for the aforementioned applied voltage Five across their plates. The capacitance C of a capacitor is defined every bit the ratio of the maximum accuse Q that can be stored in a capacitor to the applied voltage V beyond its plates. In other words, capacitance is the largest corporeality of charge per volt that can be stored on the device:

$C=\frac{Q}{V}.$

The SI unit of capacitance is the farad (F), named after Michael Faraday (1791–1867). Since capacitance is the accuse per unit voltage, one farad is i coulomb per ane volt, or

$1\phantom{\rule{0.2em}{0ex}}\text{F}=\frac{1\phantom{\rule{0.1em}{0ex}}\text{C}}{1\phantom{\rule{0.1em}{0ex}}\text{V}}.$

By definition, a 1.0-F capacitor is able to store one.0 C of charge (a very large amount of charge) when the potential difference between its plates is just 1.0 V. One farad is therefore a very large capacitance. Typical capacitance values range from picofarads $\left(1\phantom{\rule{0.2em}{0ex}}\text{pF}={10}^{\text{−}12}\phantom{\rule{0.2em}{0ex}}\text{F}\right)$ to millifarads $\left(1\phantom{\rule{0.2em}{0ex}}\text{mF}={10}^{\text{−}3}\phantom{\rule{0.2em}{0ex}}\text{F}\right)$ , which also includes microfarads ( $1\phantom{\rule{0.2em}{0ex}}\mu \text{F}={10}^{-6}\phantom{\rule{0.2em}{0ex}}\text{F}$ ). Capacitors tin can be produced in various shapes and sizes ((Figure)).

These are some typical capacitors used in electronic devices. A capacitor's size is not necessarily related to its capacitance value. (credit: Windell Oskay)

A photograph of different types of capacitors.

Calculation of Capacitance

We tin calculate the capacitance of a pair of conductors with the standard approach that follows.

Problem-Solving Strategy: Calculating Capacitance

Assume that the capacitor has a charge Q.
Determine the electrical field 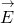$\stackrel{\to }{E}$ between the conductors. If symmetry is nowadays in the arrangement of conductors, you may be able to utilise Gauss'due south police for this calculation.
Find the potential deviation betwixt the conductors from

${V}_{B}-{V}_{A}=\text{−}\underset{A}{\overset{B}{\int }}\stackrel{\to }{E}·d\stackrel{\to }{l},$

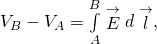
where the path of integration leads from one conductor to the other. The magnitude of the potential deviation is and then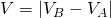 $V=|{V}_{B}-{V}_{A}|$ .
With V known, obtain the capacitance directly from (Figure).

To show how this procedure works, nosotros now calculate the capacitances of parallel-plate, spherical, and cylindrical capacitors. In all cases, we presume vacuum capacitors (empty capacitors) with no dielectric substance in the space betwixt conductors.

Parallel-Plate Capacitor

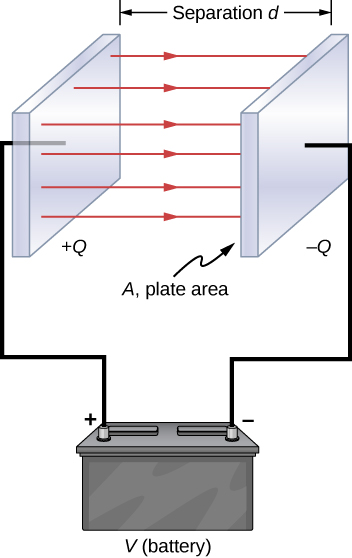
The parallel-plate capacitor ((Figure)) has two identical conducting plates, each having a surface surface area A, separated past a distance d. When a voltage V is applied to the capacitor, it stores a charge Q, as shown. Nosotros can see how its capacitance may depend on A and d by considering characteristics of the Coulomb force. We know that forcefulness between the charges increases with charge values and decreases with the distance between them. Nosotros should await that the bigger the plates are, the more accuse they can shop. Thus, C should exist greater for a larger value of A. Similarly, the closer the plates are together, the greater the attraction of the opposite charges on them. Therefore, C should be greater for a smaller d.

In a parallel-plate capacitor with plates separated past a distance d, each plate has the aforementioned surface surface area A.

Figure shows two parallel plates separated by a distance of d, with each one connected to one terminal of a battery. Electric field lines are shown as arrows from the positive plate to the negative one. The plate area is labeled A.

Nosotros define the surface charge density $\sigma$ on the plates every bit

$\sigma =\frac{Q}{A}.$

We know from previous chapters that when d is small, the electrical field betwixt the plates is fairly uniform (ignoring border effects) and that its magnitude is given by

$E=\frac{\sigma }{{\epsilon }_{0}},$

where the constant ${\epsilon }_{0}$ is the permittivity of free space, ${\epsilon }_{0}=8.85\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-12}\phantom{\rule{0.2em}{0ex}}\text{F/m}\text{.}$ The SI unit of F/g is equivalent to ${\text{C}}^{2}\text{/}\text{N}·{\text{m}}^{2}.$ Since the electrical field $\stackrel{\to }{E}$ between the plates is uniform, the potential difference betwixt the plates is

$V=Ed=\frac{\sigma d}{{\epsilon }_{0}}=\frac{Qd}{{\epsilon }_{0}A}.$

Therefore (Figure) gives the capacitance of a parallel-plate capacitor as

$C=\frac{Q}{V}=\frac{Q}{Qd\text{/}{\epsilon }_{0}A}={\epsilon }_{0}\frac{A}{d}.$

Observe from this equation that capacitance is a part but of the geometry and what textile fills the infinite betwixt the plates (in this case, vacuum) of this capacitor. In fact, this is truthful not only for a parallel-plate capacitor, but for all capacitors: The capacitance is independent of Q or V. If the charge changes, the potential changes correspondingly so that Q/V remains abiding.

Capacitance and Charge Stored in a Parallel-Plate Capacitor (a) What is the capacitance of an empty parallel-plate capacitor with metal plates that each have an area of $1.00\phantom{\rule{0.2em}{0ex}}{\text{m}}^{2}$ , separated by 1.00 mm? (b) How much charge is stored in this capacitor if a voltage of $3.00\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{3}\phantom{\rule{0.2em}{0ex}}\text{V}$ is applied to information technology?

Strategy Finding the capacitance C is a straightforward awarding of (Figure). Once nosotros find C, we can notice the charge stored by using (Effigy).

Solution

Entering the given values into (Figure) yields

$C={\epsilon }_{0}\frac{A}{d}=\left(8.85\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-12}\phantom{\rule{0.1em}{0ex}}\frac{\text{F}}{\text{m}}\right)\phantom{\rule{0.2em}{0ex}}\frac{1.00\phantom{\rule{0.2em}{0ex}}{\text{m}}^{2}}{1.00\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-3}\phantom{\rule{0.2em}{0ex}}\text{m}}=8.85\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-9}\phantom{\rule{0.2em}{0ex}}\text{F}=8.85\phantom{\rule{0.2em}{0ex}}\text{nF}\text{.}$

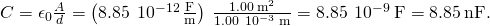
This small capacitance value indicates how difficult it is to brand a device with a large capacitance.
Inverting (Figure) and inbound the known values into this equation gives

$Q=CV=\left(8.85\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-9}\phantom{\rule{0.2em}{0ex}}\text{F}\right)\left(3.00\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{3}\phantom{\rule{0.2em}{0ex}}\text{V}\right)=26.6\phantom{\rule{0.2em}{0ex}}\mu \text{C}\text{.}$

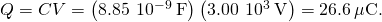
Significance This charge is simply slightly greater than those plant in typical static electricity applications. Since air breaks downwardly (becomes conductive) at an electric field force of about 3.0 MV/m, no more than accuse tin can be stored on this capacitor by increasing the voltage.

A ane-F Parallel-Plate Capacitor Suppose yous wish to construct a parallel-plate capacitor with a capacitance of ane.0 F. What area must you lot use for each plate if the plates are separated past 1.0 mm?

Solution Rearranging (Effigy), nosotros obtain

$A=\frac{Cd}{{\epsilon }_{0}}=\frac{\left(1.0\phantom{\rule{0.2em}{0ex}}\text{F}\right)\left(1.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-3}\phantom{\rule{0.2em}{0ex}}\text{m}\right)}{8.85\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-12}\phantom{\rule{0.2em}{0ex}}\text{F}\text{/}\text{m}}=1.1\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{8}\phantom{\rule{0.2em}{0ex}}{\text{m}}^{2}.$

Each foursquare plate would have to exist x km across. Information technology used to be a common prank to inquire a pupil to go to the laboratory stockroom and request a 1-F parallel-plate capacitor, until stockroom attendants got tired of the joke.

Bank check Your Understanding The capacitance of a parallel-plate capacitor is 2.0 pF. If the surface area of each plate is $2.4\phantom{\rule{0.2em}{0ex}}{\text{cm}}^{2}$ , what is the plate separation?

$1.1\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-3}\phantom{\rule{0.2em}{0ex}}\text{m}$

Check Your Understanding Verify that $\sigma \text{/}V$ and ${\epsilon }_{0}\text{/}d$ take the aforementioned physical units.

Spherical Capacitor

A spherical capacitor is another set of conductors whose capacitance tin can exist easily determined ((Effigy)). It consists of 2 concentric conducting spherical shells of radii ${R}_{1}$ (inner shell) and ${R}_{2}$ (outer shell). The shells are given equal and opposite charges $+Q$ and $\text{−}Q$ , respectively. From symmetry, the electrical field betwixt the shells is directed radially outward. We can obtain the magnitude of the field by applying Gauss'southward police force over a spherical Gaussian surface of radius r concentric with the shells. The enclosed charge is $+Q$ ; therefore nosotros accept

$\underset{S}{\oint }\stackrel{\to }{E}·\stackrel{^}{n}dA=E\left(4\pi {r}^{2}\right)=\frac{Q}{{\epsilon }_{0}}.$

Thus, the electric field between the conductors is

$\stackrel{\to }{E}=\frac{1}{4\pi {\epsilon }_{0}}\phantom{\rule{0.2em}{0ex}}\frac{Q}{{r}^{2}}\stackrel{^}{r}.$

We substitute this $\stackrel{\to }{E}$ into (Effigy) and integrate along a radial path between the shells:

$V={\int }_{{R}_{1}}^{{R}_{2}}\stackrel{\to }{E}·d\stackrel{\to }{l}={\int }_{{R}_{1}}^{{R}_{2}}\left(\frac{1}{4\pi {\epsilon }_{0}}\phantom{\rule{0.2em}{0ex}}\frac{Q}{{r}^{2}}\stackrel{^}{r}\right)·\left(\stackrel{^}{r}\text{ }dr\right)=\frac{Q}{4\pi {\epsilon }_{0}}{\int }_{{R}_{1}}^{{R}_{2}}\frac{dr}{{r}^{2}}=\frac{Q}{4\pi {\epsilon }_{0}}\left(\frac{1}{{R}_{1}}-\frac{1}{{R}_{2}}\right).$

In this equation, the potential difference betwixt the plates is $V=\text{−}\left({V}_{2}-{V}_{1}\right)={V}_{1}-{V}_{2}$ . Nosotros substitute this result into (Figure) to notice the capacitance of a spherical capacitor:

$C=\frac{Q}{V}=4\pi {\epsilon }_{0}\frac{{R}_{1}{R}_{2}}{{R}_{2}-{R}_{1}}.$

A spherical capacitor consists of two concentric conducting spheres. Note that the charges on a conductor reside on its surface.

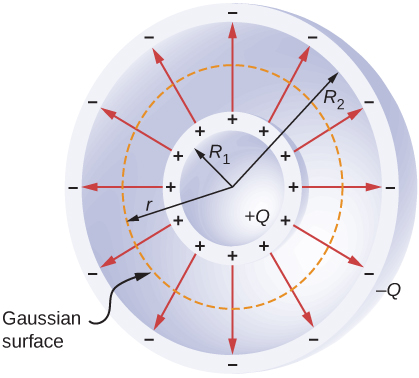
Capacitance of an Isolated Sphere Calculate the capacitance of a single isolated conducting sphere of radius ${R}_{1}$ and compare information technology with (Figure) in the limit as ${R}_{2}\to \infty$ .

Strategy We assume that the charge on the sphere is Q, so we follow the four steps outlined before. We also assume the other conductor to be a concentric hollow sphere of infinite radius.

Solution On the exterior of an isolated conducting sphere, the electrical field is given by (Effigy). The magnitude of the potential difference between the surface of an isolated sphere and infinity is

$V={\int }_{{R}_{1}}^{+\infty }\stackrel{\to }{E}·d\stackrel{\to }{l}=\frac{Q}{4\pi {\epsilon }_{0}}{\int }_{{R}_{1}}^{+\infty }\frac{1}{{r}^{2}}\stackrel{^}{r}·\left(\stackrel{^}{r}\phantom{\rule{0.2em}{0ex}}dr\right)=\frac{Q}{4\pi {\epsilon }_{0}}{\int }_{{R}_{1}}^{+\infty }\frac{dr}{{r}^{2}}=\frac{1}{4\pi {\epsilon }_{0}}\phantom{\rule{0.2em}{0ex}}\frac{Q}{{R}_{1}}.$

The capacitance of an isolated sphere is therefore

$C=\frac{Q}{V}=Q\frac{4\pi {\epsilon }_{0}{R}_{1}}{Q}=4\pi {\epsilon }_{0}{R}_{1}.$

Significance The same issue can be obtained by taking the limit of (Figure) as ${R}_{2}\to \infty$ . A unmarried isolated sphere is therefore equivalent to a spherical capacitor whose outer shell has an infinitely large radius.

Bank check Your Agreement The radius of the outer sphere of a spherical capacitor is v times the radius of its inner beat out. What are the dimensions of this capacitor if its capacitance is 5.00 pF?

3.59 cm, 17.98 cm

Cylindrical Capacitor

A cylindrical capacitor consists of ii concentric, conducting cylinders ((Figure)). The inner cylinder, of radius ${R}_{1}$ , may either exist a beat out or be completely solid. The outer cylinder is a shell of inner radius ${R}_{2}$ . We assume that the length of each cylinder is 50 and that the excess charges $+Q$ and $\text{−}Q$ reside on the inner and outer cylinders, respectively.

A cylindrical capacitor consists of two concentric, conducting cylinders. Here, the charge on the outer surface of the inner cylinder is positive (indicated past $+$ ) and the accuse on the inner surface of the outer cylinder is negative (indicated by $-$ ).

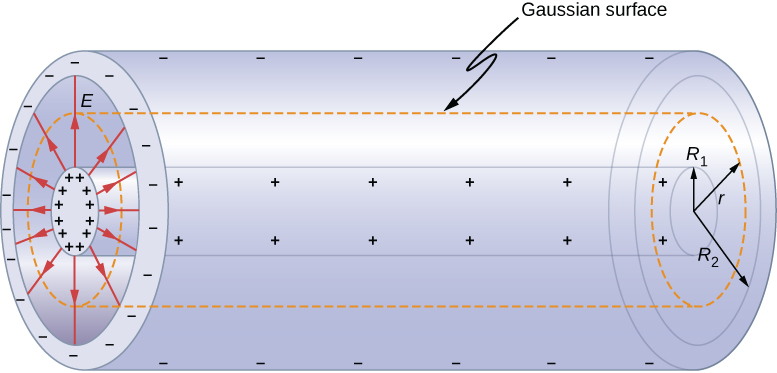
Figure shows two concentric cylinders. The inner one, with radius R1 has positive signs on it. The outer one, with radius R2 has negative signs on it. Arrows marked E are shown radiating from the inner one to the outer one. A third cylinder, with radius r, is shown as a dotted line between the two. This is labeled Gaussian surface.

With edge furnishings ignored, the electric field between the conductors is directed radially outward from the common centrality of the cylinders. Using the Gaussian surface shown in (Figure), we have

$\underset{S}{\oint }\stackrel{\to }{E}·\stackrel{^}{n}\phantom{\rule{0.2em}{0ex}}dA=E\left(2\pi rl\right)=\frac{Q}{{\epsilon }_{0}}.$

Therefore, the electric field betwixt the cylinders is

$\stackrel{\to }{E}=\frac{1}{2\pi {\epsilon }_{0}}\phantom{\rule{0.2em}{0ex}}\frac{Q}{r\phantom{\rule{0.2em}{0ex}}l}\stackrel{^}{r}.$

Here $\stackrel{^}{r}$ is the unit radial vector along the radius of the cylinder. Nosotros can substitute into (Figure) and find the potential departure between the cylinders:

$V={\int }_{{R}_{1}}^{{R}_{2}}\stackrel{\to }{E}·d{\stackrel{\to }{l}}_{p}=\frac{Q}{2\pi {\epsilon }_{0}\phantom{\rule{0.2em}{0ex}}l}{\int }_{{R}_{1}}^{{R}_{2}}\frac{1}{r}\stackrel{^}{r}·\left(\stackrel{^}{r}\phantom{\rule{0.2em}{0ex}}dr\right)=\frac{Q}{2\pi {\epsilon }_{0}\phantom{\rule{0.2em}{0ex}}l}{\int }_{{R}_{1}}^{{R}_{2}}\frac{dr}{r}=\frac{Q}{2\pi {\epsilon }_{0}\phantom{\rule{0.2em}{0ex}}l}{\text{ln}r|}_{{R}_{1}}^{{R}_{2}}=\frac{Q}{2\pi {\epsilon }_{0}\phantom{\rule{0.2em}{0ex}}l}\text{ln}\frac{{R}_{2}}{{R}_{1}}.$

Thus, the capacitance of a cylindrical capacitor is

$C=\frac{Q}{V}=\frac{2\pi {\epsilon }_{0}\phantom{\rule{0.2em}{0ex}}l}{\text{ln}\left({R}_{2}\text{/}{R}_{1}\right)}.$

Every bit in other cases, this capacitance depends only on the geometry of the conductor system. An important application of (Effigy) is the determination of the capacitance per unit length of a coaxial cablevision, which is commonly used to transmit time-varying electric signals. A coaxial cablevision consists of two concentric, cylindrical conductors separated past an insulating fabric. (Here, we assume a vacuum betwixt the conductors, but the physics is qualitatively nearly the aforementioned when the space betwixt the conductors is filled by a dielectric.) This configuration shields the electrical signal propagating downwards the inner usher from devious electric fields external to the cable. Current flows in contrary directions in the inner and the outer conductors, with the outer conductor commonly grounded. Now, from (Figure), the capacitance per unit length of the coaxial cable is given by

$\frac{C}{l}=\frac{2\pi {\epsilon }_{0}}{\text{ln}\left({R}_{2}\text{/}{R}_{1}\right)}.$

In practical applications, it is of import to select specific values of C/fifty. This tin can be achieved with appropriate choices of radii of the conductors and of the insulating cloth between them.

Cheque Your Understanding When a cylindrical capacitor is given a charge of 0.500 nC, a potential difference of 20.0 V is measured betwixt the cylinders. (a) What is the capacitance of this system? (b) If the cylinders are 1.0 thousand long, what is the ratio of their radii?

a. 25.0 pF; b. 9.ii

Several types of practical capacitors are shown in (Figure). Mutual capacitors are ofttimes made of ii small pieces of metallic foil separated by 2 small pieces of insulation (meet (Effigy)(b)). The metal foil and insulation are encased in a protective coating, and two metallic leads are used for connecting the foils to an external circuit. Some common insulating materials are mica, ceramic, paper, and Teflon™ non-stick coating.

Another popular type of capacitor is an electrolytic capacitor. It consists of an oxidized metal in a conducting paste. The master advantage of an electrolytic capacitor is its high capacitance relative to other mutual types of capacitors. For example, capacitance of one type of aluminum electrolytic capacitor can be as high as 1.0 F. However, yous must be careful when using an electrolytic capacitor in a circuit, because information technology but functions correctly when the metal foil is at a higher potential than the conducting paste. When reverse polarization occurs, electrolytic action destroys the oxide film. This blazon of capacitor cannot be connected beyond an alternating current source, because half of the time, ac voltage would accept the wrong polarity, as an alternating current reverses its polarity (see Alternating-Current Circuts on alternate-current circuits).

A variable air capacitor ((Effigy)) has ii sets of parallel plates. 1 set of plates is stock-still (indicated as "stator"), and the other fix of plates is attached to a shaft that can be rotated (indicated as "rotor"). By turning the shaft, the cross-sectional area in the overlap of the plates can be changed; therefore, the capacitance of this system can be tuned to a desired value. Capacitor tuning has applications in any type of radio transmission and in receiving radio signals from electronic devices. Any time you tune your car radio to your favorite station, call back of capacitance.

In a variable air capacitor, capacitance can be tuned by changing the constructive surface area of the plates. (credit: modification of work past Robbie Sproule)

A photograph of a device with discrete components is shown. One component is the variable air capacitor. It has two parts, a stator and a rotor. The stator has parallel plates of metal and is fixed to the device. The rotor has parallel plates of metal attached to a shaft. The stator and rotor are arranged in a way that their plates are alternately stacked.

The symbols shown in (Figure) are circuit representations of diverse types of capacitors. We by and large use the symbol shown in (Figure)(a). The symbol in (Figure)(c) represents a variable-capacitance capacitor. Notice the similarity of these symbols to the symmetry of a parallel-plate capacitor. An electrolytic capacitor is represented by the symbol in part (Figure)(b), where the curved plate indicates the negative last.

This shows three different circuit representations of capacitors. The symbol in (a) is the most commonly used i. The symbol in (b) represents an electrolytic capacitor. The symbol in (c) represents a variable-capacitance capacitor.

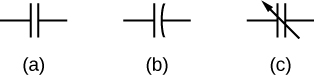
Figure a shows two vertical lines. Figure b shows a vertical line to the left and another, slightly curved vertical line to the right. Figure c shows two vertical lines and an arrow cutting across them diagonally. In all figures, each line is connected to a horizontal line on the outside.

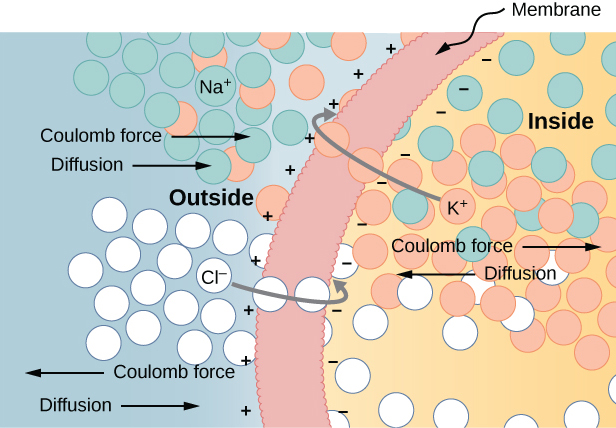
An interesting applied example of a capacitor model comes from cell biology and deals with the electrical potential in the plasma membrane of a living cell ((Figure)). Cell membranes separate cells from their surroundings merely allow some selected ions to laissez passer in or out of the cell. The potential departure across a membrane is nigh 70 mV. The cell membrane may be 7 to ten nm thick. Treating the cell membrane as a nano-sized capacitor, the estimate of the smallest electric field forcefulness across its 'plates' yields the value $E=\frac{V}{d}=\frac{70\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-3}\text{V}}{10\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-9}\text{m}}=7\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{6}\phantom{\rule{0.2em}{0ex}}\text{V/m}\phantom{\rule{0.2em}{0ex}}>3\phantom{\rule{0.2em}{0ex}}\text{MV/m}$ .

This magnitude of electric field is smashing enough to create an electrical spark in the air.

The semipermeable membrane of a biological jail cell has different concentrations of ions on its interior surface than on its exterior. Diffusion moves the ${\text{K}}^{\text{+}}$ (potassium) and ${\text{Cl}}^{\text{-}}$ (chloride) ions in the directions shown, until the Coulomb force halts farther transfer. In this way, the outside of the membrane acquires a positive charge and its interior surface acquires a negative charge, creating a potential difference across the membrane. The membrane is ordinarily impermeable to Na+ (sodium ions).

Visit the PhET Explorations: Capacitor Lab to explore how a capacitor works. Change the size of the plates and add a dielectric to meet the result on capacitance. Change the voltage and come across charges built upwards on the plates. Observe the electric field in the capacitor. Measure the voltage and the electric field.

Summary

A capacitor is a device that stores an electrical accuse and electrical free energy. The amount of accuse a vacuum capacitor can shop depends on ii major factors: the voltage applied and the capacitor's physical characteristics, such as its size and geometry.
The capacitance of a capacitor is a parameter that tells united states how much charge can be stored in the capacitor per unit potential difference between its plates. Capacitance of a organization of conductors depends but on the geometry of their arrangement and physical properties of the insulating cloth that fills the space between the conductors. The unit of capacitance is the farad, where $1\phantom{\rule{0.2em}{0ex}}\text{F}=1\phantom{\rule{0.2em}{0ex}}\text{C}\text{/}1\phantom{\rule{0.2em}{0ex}}\text{V}.$

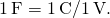
Conceptual Questions

Does the capacitance of a device depend on the applied voltage? Does the capacitance of a device depend on the charge residing on it?

no; yes

Would you place the plates of a parallel-plate capacitor closer together or farther autonomously to increment their capacitance?

The value of the capacitance is zero if the plates are not charged. Truthful or fake?

false

If the plates of a capacitor have different areas, will they acquire the same charge when the capacitor is connected across a bombardment?

Does the capacitance of a spherical capacitor depend on which sphere is charged positively or negatively?

Problems

What charge is stored in a $180.0\text{-}\mu \text{F}$ capacitor when 120.0 Five is applied to it?

21.6 mC

Find the charge stored when v.l Five is practical to an 8.00-pF capacitor.

Calculate the voltage applied to a $2.00\text{-}\mu \text{F}$ capacitor when it holds $3.10\phantom{\rule{0.2em}{0ex}}\mu \text{C}$ of accuse.

1.55 5

What voltage must be practical to an 8.00-nF capacitor to store 0.160 mC of charge?

What capacitance is needed to store $3.00\phantom{\rule{0.2em}{0ex}}\mu \text{C}$ of charge at a voltage of 120 V?

25.0 nF

What is the capacitance of a large Van de Graaff generator's terminal, given that it stores 8.00 mC of accuse at a voltage of 12.0 MV?

The plates of an empty parallel-plate capacitor of capacitance v.0 pF are two.0 mm apart. What is the area of each plate?

$1.1\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-3}{\text{m}}^{2}$

A 60.0-pF vacuum capacitor has a plate area of $0.010\phantom{\rule{0.2em}{0ex}}{\text{m}}^{2}$ . What is the separation betwixt its plates?

A set of parallel plates has a capacitance of $5.0\text{µ}\text{F}$ . How much charge must be added to the plates to increment the potential difference between them by 100 5?

500 µC

Consider Earth to be a spherical usher of radius 6400 km and calculate its capacitance.

If the capacitance per unit length of a cylindrical capacitor is 20 pF/m, what is the ratio of the radii of the ii cylinders?

i:16

An empty parallel-plate capacitor has a capacitance of $20\phantom{\rule{0.2em}{0ex}}µ\text{F}$ . How much charge must leak off its plates earlier the voltage across them is reduced by 100 V?

Glossary

capacitance: amount of charge stored per unit volt

capacitor: device that stores electrical charge and electric free energy

dielectric: insulating material used to fill the space between two plates

parallel-plate capacitor: system of two identical parallel conducting plates separated past a altitude

hermanemeart.blogspot.com

Source: https://opentextbc.ca/universityphysicsv2openstax/chapter/capacitors-and-capacitance/

if the charge on an isolated spherical conductor is doubled, what happens to its capacitance?

49 Capacitors and Capacitance

Learning Objectives

Calculation of Capacitance

Parallel-Plate Capacitor

Spherical Capacitor

Cylindrical Capacitor

Summary

Conceptual Questions

Problems

Glossary

0 Response to "if the charge on an isolated spherical conductor is doubled, what happens to its capacitance?"

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel